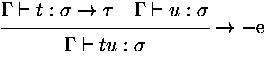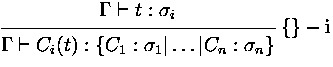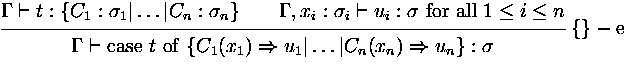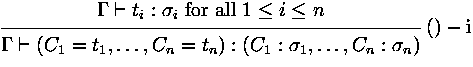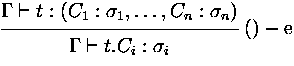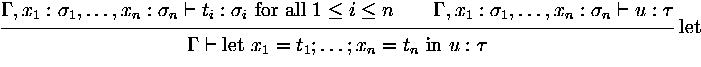Next: Examples
Up: foetus - Termination Checker
Previous: Introduction
Subsections
A foetus program consists of terms and definitions.
| P |
: : |
|
empty program |
|---|
| |
| |
term; P |
term to be evaluated |
| |
| |
definition; P |
definition for further use |
When processing input, foetus evaluates the terms and stores the
definitions in the environment. ``Reserved words'' in the foetus language are case, of, let and in.
Special characterss are ( ) [ ] { } | . , ; = =>. An identifier may
contain letters, digits, apostrophies and underscores.
If it starts with a small letter it stands for a variable,
else it denotes a constant.
In the following
x , x1 , x2 , ... denote variables,
C , C1 , C2 , ... constants and
u , t , t1 , t2 , ... foetus terms.
| t |
: : |
x |
variable |
|---|
| |
| |
[x]t |
lambda |
| |
| |
tu |
application |
| |
| |
C(t) |
constructor |
| |
| |
case t of {
C1x1  t1|...|Cnxn t1|...|Cnxn  tn } tn } |
pattern matching |
| |
| |
(C1 = t1,...,Cn = tn) |
tuple |
| |
| |
t.C |
projection |
| |
| |
let
x1 = t1,...,xn = tn in t |
let |
| |
| |
(t) |
(extra parentheses) |
A definition statement has the form
x1 = t1,...,xn = tn (it
is a let-term without a ``body''). All variables
x1,...,xn are
defined simultanously, thus can refer to each other.
The following foetus program defines addition
on natural numbers (spanned by the two constructors O ``zero'' and
S ``successor'') and calculates 1 + 1 .
add = [x][y]case x of
{ O z => y
| S x' => S(add x' y) };
one = S(O());
add one one;
Note that although O is a zero-argument-constructor the syntax
forces us to supply a dummy variable z within the pattern
definition and also empty tuple () in the definition of one.
In the following x , x1 , x2 , ... denote variables,
C , C1 , C2 , ... constants,
u , t , t1 , t2 , ... foetus terms,
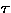 ,
, 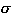 ,
, 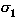 ,
, 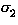 , ... foetus types and
X , X1 , X2,... type variables.
, ... foetus types and
X , X1 , X2,... type variables.
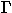 = x1 :
= x1 : 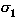 ,...,xn :
,...,xn : 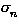 denotes the context.
The judgement
denotes the context.
The judgement
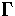
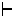 t :
t : 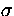
means ``in context 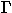 term t is of type
term t is of type 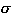 ''.
''.
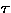 |
: : |
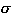 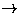 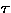 |
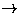 -type -type |
|---|
| |
| |
{C1 : 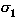 |...|Cn : |...|Cn : 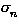 } } |
labeled sum type |
| |
| |
(C1 : 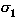 ,...,Cn : ,...,Cn : 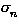 ) ) |
labeled product type |
| |
| |
{X}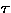 |
polymorphic type |
| |
| |
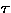 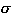 |
instantiation of polymorphic type |
| |
| |
Let X1 = 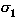 ,...,Xn = ,...,Xn = 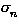 in in 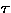 |
recursive type |
In the formation of a recursive type with Let Xi may only appear
strict positiv in 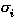 . We define congruence on types
. We define congruence on types 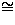 as
the smallest congruence closed under
as
the smallest congruence closed under
Let 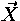 =
= 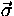 in
in 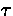
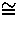
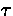 [X1 : = Let
[X1 : = Let 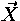 =
= 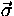 in X1;...;Xn : = Let
in X1;...;Xn : = Let 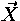 =
= 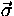 in Xn]
in Xn]
(
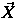 =
= 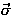 abbreviates
X1 =
abbreviates
X1 = 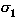 ,...,Xn =
,...,Xn = 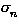 ). Thus we can substitute congruent types:
). Thus we can substitute congruent types:
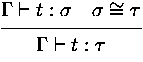
For ploymorphic types we have rules like in System F:
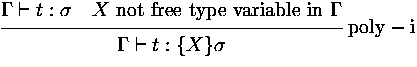
![$\displaystyle
\rux {\Gamma\vdash t: \{X\}\sigma}
{\Gamma\vdash t: \sigma[X:=\tau]}
{poly-e}
$](img22.gif)
We here only briefly introduce the typing rules. For more detailed
explanation, read a book about type theorie, e.g. [NPS90].
![$\displaystyle
\rux {\Gamma,x:\sigma \vdash t:\tau}
{\Gamma\vdash [x]t : \sigma \rightarrow \tau}
{\rightarrow-i}
$](img23.gif)
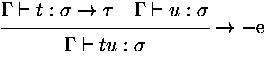
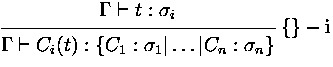
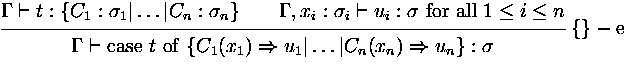
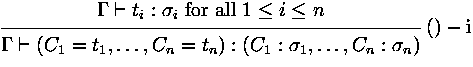
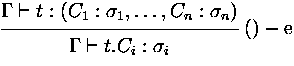
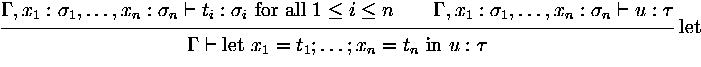
In foetus type checking is not yet implemented and it is assummed
that all terms entered are well typed. Of course, only for well typed
terms the termination check produces valid results.
The following well-known example for
non-termination passes the foetus termination checker, but it is not
well typed.
f = [x]x x;
a = f f;
foetus output:
f passes termination check
a passes termination check
Run example.



Next: Examples
Up: foetus - Termination Checker
Previous: Introduction
Andreas Abel, 7/16/1998
![]()
![]() t :
t : ![]()
![]() =
= ![]() in
in ![]()
![]()
![]() [X1 : = Let
[X1 : = Let ![]() =
= ![]() in X1;...;Xn : = Let
in X1;...;Xn : = Let ![]() =
= ![]() in Xn]
in Xn]
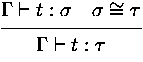
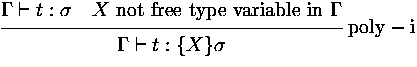
![$\displaystyle
\rux {\Gamma\vdash t: \{X\}\sigma}
{\Gamma\vdash t: \sigma[X:=\tau]}
{poly-e}
$](img22.gif)
![$\displaystyle
\rux {\Gamma,x:\sigma \vdash t:\tau}
{\Gamma\vdash [x]t : \sigma \rightarrow \tau}
{\rightarrow-i}
$](img23.gif)