


Next: Implementation
Up: foetus - Termination Checker
Previous: Termination Checker Overall Outline
Subsections
Be
R = {` < ',` = ',`?'} set of the relations ``less
than'', ``equal to'' and ``relation unknown''. In the context of
`` f (x,y) calls g(a,b) ''
a ` < ' y means ``we know that (call)
argument a is less than (input) parameter y '',
a ` = ' y means
`` a is (at least) equal to y (if not less than)'' and a `?' y means ``we do not know the relation between a and y ''.
With the two operations
+ and 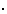 defined as in table 1 R forms a
commutative
rig
defined as in table 1 R forms a
commutative
rig![[*]](http://www.tcs.informatik.uni-muenchen.de/icons/foot_motif.gif) with 0-element `?' and 1 -element ` = ' . The operation + can be
understood as ``combining parallel information about a relation'',
e.g. if we have a `?' y and
a ` < ' y we have
a (`?' + ` < ') y and that simplifies to
a ` < ' y .
The operation
with 0-element `?' and 1 -element ` = ' . The operation + can be
understood as ``combining parallel information about a relation'',
e.g. if we have a `?' y and
a ` < ' y we have
a (`?' + ` < ') y and that simplifies to
a ` < ' y .
The operation
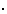 however is ``serial combination'', e.g.
a ` < ' y
and
y ` = ' z can be combined into
a (` < '
however is ``serial combination'', e.g.
a ` < ' y
and
y ` = ' z can be combined into
a (` < ' 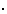 ` = ') z ,
simplified:
a ` < ' z . `?' is neutral regarding + because
it gives you no new information, whereas ` < ' is dominant because
it is the strongest information. Regarding
` = ') z ,
simplified:
a ` < ' z . `?' is neutral regarding + because
it gives you no new information, whereas ` < ' is dominant because
it is the strongest information. Regarding 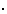 the relation
` = ' is neutral
and `?' is dominant because it ``destroys'' all
information. Check the table to see which relation overrides which.
the relation
` = ' is neutral
and `?' is dominant because it ``destroys'' all
information. Check the table to see which relation overrides which.
Table 1:
Operations on R
| + |
` < ' |
` = ' |
`?' |
| ` < ' |
` < ' |
` < ' |
` < ' |
| ` = ' |
` < ' |
` = ' |
` = ' |
| `?' |
` < ' |
` = ' |
`?' |
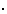 |
` < ' |
` = ' |
`?' |
| ` < ' |
` < ' |
` < ' |
`?' |
| ` = ' |
` < ' |
` = ' |
`?' |
| `?' |
`?' |
`?' |
`?' |
Now we can define multiplication on matrices over R as usual:
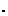 : R n x m x R m x l
: R n x m x R m x l 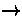 R n x l
R n x l
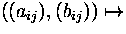 (cij) =
(cij) = 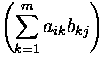
Why is this a reasonable definition? Assume you have three sets of
variables
{x1,...,xn} ,
{y1,...,ym} and
{z1,...,zl} , a matrix
A = (aij)  R n x m reflecting the
relations between the xi s and the yi s (i.d.
aij =
R n x m reflecting the
relations between the xi s and the yi s (i.d.
aij = 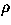
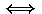 xi
xi 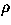 yj ) and a matrix
B
yj ) and a matrix
B  R m x l reflecting the
relations between the yi s and the zi s. Then the matrix product
C = AB reflects the relations between the xi s and the zi s. Because
R m x l reflecting the
relations between the yi s and the zi s. Then the matrix product
C = AB reflects the relations between the xi s and the zi s. Because
cij = ai1 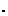 b1j + ai2
b1j + ai2 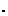 b2j + ... + aim
b2j + ... + aim 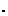 bmj,
bmj,
we have e.g.
xi ` < ' zj if we know it by intermediate variable y1
(
ai1 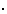 b1j = ` < ' ) or by intermediate variable
y2 or ... (to be continued).
A call matrix is a matrix over R with no more than one element
different from `?' per row.
b1j = ` < ' ) or by intermediate variable
y2 or ... (to be continued).
A call matrix is a matrix over R with no more than one element
different from `?' per row.
CM(n,m) : = {(aij) 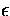 R n x m :
R n x m : 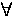 i
i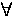 j
j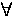 k
k 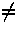 j(aij = `?'
j(aij = `?'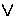 aik = `?')}
aik = `?')}
The reason we define call matrices this way is
these are the only ones foetus produces by function call extraction
(see section 4.1). Because foetus recognizes only the
three described cases of dependecies, a call argument can only depend
of one function parameter. But multiple dependecies are
imaginable, like in
f(x,y) = if (x=0) then 0 else let a=min(x,y)-1 in f(a,x)
Here the second call argument a is less than both x and
y. The next proposition assures that all matrices foetus will
have do deal with are call matrices.
Matrix multiplication on matrices induces a multiplication on call matrices
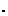 : CM(n,m) x CM(m,l )
: CM(n,m) x CM(m,l ) 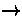 CM (n,l )
CM (n,l )
This operation is well defined.
Be
A = (aij)  CM (n,m) ,
B = (bij)
CM (n,m) ,
B = (bij)  CM (m,l ) ,
AB = C = (cij)
CM (m,l ) ,
AB = C = (cij)  R n x l and k(i) the
index of the element of the i th row of A that is different to
`?' (or 1, if no such element exists). The we have with the
rules in rig R
R n x l and k(i) the
index of the element of the i th row of A that is different to
`?' (or 1, if no such element exists). The we have with the
rules in rig R
cij = 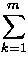 aikbkj = ai,k(i)bk(i),j
aikbkj = ai,k(i)bk(i),j
Now consider the i th row of C :
ci = (cij)1 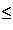 j
j 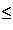 l = (ai,k(i)bk(i),j)1
l = (ai,k(i)bk(i),j)1 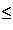 j
j 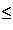 l
l
Because at most one bk(i),j is unequal to `?' , at most one
element of ci is unequal to `?' . Therefore
C  CM (n,l ) .
For each
i
CM (n,l ) .
For each
i  N we assume a set
F (i) = {f (i),g (i),h (i),...} of identifiers for functions of arity i ,
N we assume a set
F (i) = {f (i),g (i),h (i),...} of identifiers for functions of arity i ,
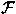 =
= 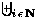 F (i).
We form the set of calls as follows
F (i).
We form the set of calls as follows
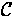 = {(f (n),g (m),A) : f (n)
= {(f (n),g (m),A) : f (n) 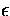 F (n),g (m)
F (n),g (m) 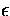 F (m),A
F (m),A 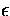 CM(m,n)}
CM(m,n)}
On calls we define the partial operation combination of calls
o : 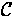 x
x 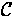
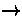
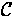
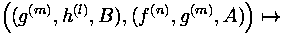 (f (n),h (l),BA)
(f (n),h (l),BA)
Meaning: If g calls h with call matrix B and f calls g with
call matrix A , then f indirectly calls h with call matrix
BA . o cannot be applied to calls that have no ``common
function'' like g , therefore it is partial. o can be expanded
to sets of calls
o : 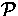 (
(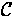 ) x
) x 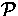 (
(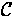 )
) 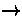
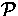 (
(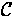 )
)
(C,C') 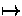 {c o
{c o 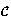 c' : c
c' : c 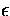 C,c'
C,c' 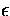 C',(c,c')
C',(c,c') 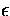 Dom( o
Dom( o 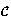 )}
)}
Here we combine each call in C with each call in 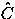 to which
o
to which
o 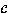 is applicable and form a set of the combined
calls.
o
is applicable and form a set of the combined
calls.
o 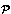 (
(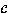 ) is a total function.
A call graph is a graph (V,E) with
vertices
V =
) is a total function.
A call graph is a graph (V,E) with
vertices
V =  F and edges
E
F and edges
E 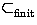
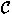 .
A call graph is complete if
.
A call graph is complete if
E o E 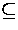 E
E
The completion of a call graph (V,E) is a call graph (V,E')
such that
- 1.
- (V,E') is complete,
- 2.
-
E
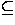 E' and
E' and - 3.
- for all E'' satisfying (1) and
(2) we have
E'
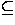 E'' .
E'' .
The completion of a call graph (V,E) is the call graph (V,E')
such that
c 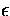 E'
E'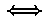
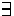 n > 0,c1,...,cn
n > 0,c1,...,cn 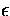 E : c1 o ... o cn = c
E : c1 o ... o cn = c
- 1.
- Be
c
 E' o E' . Then there are
d,e
E' o E' . Then there are
d,e  E' with
c = d o e . Because (V,E') is complete, we have
E' with
c = d o e . Because (V,E') is complete, we have
|
d = d1 o ... o dn
|

|
d1,...,dn 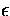 E E
| |
|
e = e1 o ... o em
|

|
e1,...,em 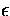 E E
| |
Thus
c = d1 o ... o dn o e1 o ... o em  E' .
E' .
- 2.
-
E
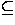 E' is trivial with n = 1 .
E' is trivial with n = 1 .
- 3.
- Be (V,E'') complete and
E
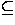 E'' . This gives us
E o E
E'' . This gives us
E o E 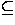 E'' from which we gain by induction
E'' from which we gain by induction
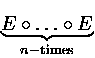 = : E n
= : E n 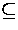 E'' for all n.
E'' for all n.
Now be
c  E' . That implies
c = c1 o ... o cn (
ci
E' . That implies
c = c1 o ... o cn (
ci  E ) for a suitable n . Hence
c
E ) for a suitable n . Hence
c  E n
E n 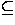 E'' .
q
E'' .
q  e
e  d
d
Be (V,E) a call graph, (V,E') its completion and
(En)n  N a sequence of sets of calls defined as follows:
N a sequence of sets of calls defined as follows:
|
E0
|
=
|
E
| |
|
En + 1
|
=
|
En 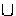 (En o E) (En o E)
| |
Then there is a
n  N so that
N so that
E' = En = En + 1 = En + 2 = ...
(Obviously the En grow monotonously.)
First we show by induction that
En 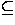 E' for all
n
E' for all
n  N : It is obvious that
E0
N : It is obvious that
E0 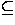 E' . Now be
En
E' . Now be
En 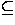 E' and
c
E' and
c  En + 1
En + 1 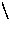 En . Then
c
En . Then
c  En o E , therefore
c = d1 o ... o dn o e ,
d1,...,dn,e
En o E , therefore
c = d1 o ... o dn o e ,
d1,...,dn,e  E . It
follows
c
E . It
follows
c  E' ,
En + 1
E' ,
En + 1 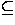 E' .
E' .
Second: Because we have a finit set of starting edges E and
therefore a finit set of reachable vertices and also a finit set of
possible edges between two vertices (limited by the number of
different call matrices of fixed dimensions) the Ei s cannot grow
endlessly. Thus an
n  N exists with
En = En + 1 .
N exists with
En = En + 1 .
Third: We show that
E' 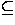 En for that particular n . Be
c
En for that particular n . Be
c  E' . Then there exists an m such that
c = d1 o ... o dm , therefore
c
E' . Then there exists an m such that
c = d1 o ... o dm , therefore
c  Em . Now if m
Em . Now if m 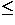 n then
Em
n then
Em 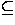 En , otherwise m > n and hence Em = En , in both cases
c
En , otherwise m > n and hence Em = En , in both cases
c  En .
q
En .
q 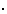 e
e 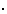 d
d
Be (V,E) a complete call graph and
f (i) a function of arity i . We call
Ef(i) : = {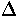 (C) : (f (i),f (i),C)
(C) : (f (i),f (i),C) 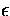 E}
E} 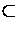 R i
R i
the recursion behaviour of function f (i). ( 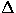 takes the
diagonal of square matrices).
takes the
diagonal of square matrices).
Each row of this set represents one possible recursive call of f (i)
and how the orders of all parameters are altered in this call. The
diagonals of the call matrices are taken because we want to know only
how a parameter relates to its old value in the last call to
f (i). Ef(i) of course is a finite subset of R i.
In the following we identify lexical orders on parameters with
permutations
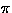
 Sn of the arguments. Often not all of the
parameters are relevant for termination; these are not listed in the
lexical order and can appear in the permutation in any sequence.
Sn of the arguments. Often not all of the
parameters are relevant for termination; these are not listed in the
lexical order and can appear in the permutation in any sequence.
In example 3.11 (fib') only the argument 0 has to be
considered to prove termination, the order of argument 1 and 2 are
irrelevant and therefore both permutations
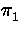 =
= 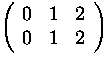
and
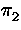 =
= 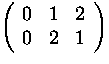
are valid continuations of the lexical order ``0''.
In the following we abbreviate the notation of permutations to
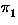 = [012] and
= [012] and
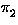 = [021] .
Be B the recursion behaviour of function f (n).
We call the permutation
= [021] .
Be B the recursion behaviour of function f (n).
We call the permutation
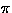
 Sn a termination order for
f (n) if
Sn a termination order for
f (n) if
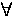 r
r 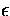 B
B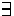 1
1 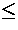 k
k 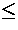 n : r
n : r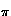 (k) = ` < '
(k) = ` < '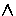 (
(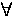 1
1 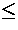 i
i 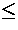 k : r
k : r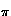 (i) = ` = ')
(i) = ` = ')
This definition is a very wide one. In most cases you will look for
more special termination orders:
Be B the recursion behaviour of a given function.
We call the permutation
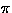
 Sn a termination order on B
if |B| = 0 or
Sn a termination order on B
if |B| = 0 or
|
|
|
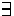 r r 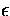 B : r B : r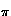 (0) = ` < ' (0) = ` < '
| |
|
|
|
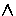 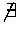 r r 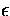 B : r B : r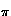 (0) = `?' (0) = `?'
| |
|
|
|
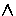 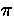 ' ' 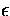 Sn - 1 termination order on B' : = {r' Sn - 1 termination order on B' : = {r'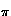 (0) : r (0) : r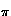 (0) (0) 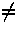 ` < '} ` < '} 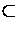 R n - 1 R n - 1
| |
whereas
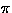 'i = [k0...ki - 1ki + 1...kn - 1]
'i = [k0...ki - 1ki + 1...kn - 1]  Sn - 1 given
Sn - 1 given
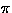 = [k0...kn - 1]
= [k0...kn - 1]  Sn and
r'i = (k0,...,ki - 1,ki + 1,...,kn - 1)
Sn and
r'i = (k0,...,ki - 1,ki + 1,...,kn - 1)  R n - 1 given
r = (k0,...,kn - 1)
R n - 1 given
r = (k0,...,kn - 1)  R n.
R n.
The algorithm implemented in foetus searches termination orders
like in definition (2); it is a one-to-one transfer of this
definition. Every termination order matching definition (2) also
matches definition (1) and it can easily be shown that if there is a
termination order of type (1) there also exists on of type (2).
Example 2986
Be
E = {(` = ',` < ',`?'),(` = ',` = ',` < '),(` = ',` < ',` = ')} the given recursion behaviour. Then
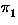 = [012] is a type (1) termination order on E and
= [012] is a type (1) termination order on E and
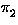 = [120] is of
both types.
= [120] is of
both types.



Next: Implementation
Up: foetus - Termination Checker
Previous: Termination Checker Overall Outline
Andreas Abel, 7/16/1998
![]() defined as in table 1 R forms a
commutative
rig
defined as in table 1 R forms a
commutative
rig![]() with 0-element `?' and 1 -element ` = ' . The operation + can be
understood as ``combining parallel information about a relation'',
e.g. if we have a `?' y and
a ` < ' y we have
a (`?' + ` < ') y and that simplifies to
a ` < ' y .
The operation
with 0-element `?' and 1 -element ` = ' . The operation + can be
understood as ``combining parallel information about a relation'',
e.g. if we have a `?' y and
a ` < ' y we have
a (`?' + ` < ') y and that simplifies to
a ` < ' y .
The operation
![]() however is ``serial combination'', e.g.
a ` < ' y
and
y ` = ' z can be combined into
a (` < '
however is ``serial combination'', e.g.
a ` < ' y
and
y ` = ' z can be combined into
a (` < ' ![]() ` = ') z ,
simplified:
a ` < ' z . `?' is neutral regarding + because
it gives you no new information, whereas ` < ' is dominant because
it is the strongest information. Regarding
` = ') z ,
simplified:
a ` < ' z . `?' is neutral regarding + because
it gives you no new information, whereas ` < ' is dominant because
it is the strongest information. Regarding ![]() the relation
` = ' is neutral
and `?' is dominant because it ``destroys'' all
information. Check the table to see which relation overrides which.
the relation
` = ' is neutral
and `?' is dominant because it ``destroys'' all
information. Check the table to see which relation overrides which.
![]() : R n x m x R m x l
: R n x m x R m x l ![]() R n x l
R n x l
![]() (cij) =
(cij) = 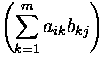
![]() b1j + ai2
b1j + ai2 ![]() b2j + ... + aim
b2j + ... + aim ![]() bmj,
bmj,
![]() R n x m :
R n x m : ![]() i
i![]() j
j![]() k
k ![]() j(aij = `?'
j(aij = `?'![]() aik = `?')}
aik = `?')}
![]() : CM(n,m) x CM(m,l )
: CM(n,m) x CM(m,l ) ![]() CM (n,l )
CM (n,l )
![]() aikbkj = ai,k(i)bk(i),j
aikbkj = ai,k(i)bk(i),j
![]() j
j ![]() l = (ai,k(i)bk(i),j)1
l = (ai,k(i)bk(i),j)1 ![]() j
j ![]() l
l
![]() = {(f (n),g (m),A) : f (n)
= {(f (n),g (m),A) : f (n) ![]() F (n),g (m)
F (n),g (m) ![]() F (m),A
F (m),A ![]() CM(m,n)}
CM(m,n)}
![]() x
x ![]()
![]()
![]()
![]() (f (n),h (l),BA)
(f (n),h (l),BA)
![]() (
(![]() ) x
) x ![]() (
(![]() )
) ![]()
![]() (
(![]() )
)
![]() {c o
{c o ![]() c' : c
c' : c ![]() C,c'
C,c' ![]() C',(c,c')
C',(c,c') ![]() Dom( o
Dom( o ![]() )}
)}
![]() E
E
![]() E'
E'![]()
![]() n > 0,c1,...,cn
n > 0,c1,...,cn ![]() E : c1 o ... o cn = c
E : c1 o ... o cn = c
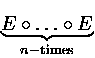 = : E n
= : E n ![]() E'' for all n.
E'' for all n.
![]() N exists with
En = En + 1 .
N exists with
En = En + 1 .
![]() En for that particular n . Be
c
En for that particular n . Be
c ![]() E' . Then there exists an m such that
c = d1 o ... o dm , therefore
c
E' . Then there exists an m such that
c = d1 o ... o dm , therefore
c ![]() Em . Now if m
Em . Now if m ![]() n then
Em
n then
Em ![]() En , otherwise m > n and hence Em = En , in both cases
c
En , otherwise m > n and hence Em = En , in both cases
c ![]() En .
q
En .
q ![]() e
e ![]() d
d ![]() (C) : (f (i),f (i),C)
(C) : (f (i),f (i),C) ![]() E}
E} ![]() R i
R i
![]()
![]() Sn of the arguments. Often not all of the
parameters are relevant for termination; these are not listed in the
lexical order and can appear in the permutation in any sequence.
Sn of the arguments. Often not all of the
parameters are relevant for termination; these are not listed in the
lexical order and can appear in the permutation in any sequence.
![]() =
= 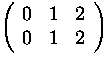
![]() =
= 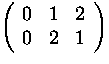
![]() r
r ![]() B
B![]() 1
1 ![]() k
k ![]() n : r
n : r![]() (k) = ` < '
(k) = ` < '![]() (
(![]() 1
1 ![]() i
i ![]() k : r
k : r![]() (i) = ` = ')
(i) = ` = ')
![]() = [012] is a type (1) termination order on E and
= [012] is a type (1) termination order on E and
![]() = [120] is of
both types.
= [120] is of
both types.